原标题:上课听不懂,做题没思路……孩子遇上“数学困难症” 本质都是这2点出了问题
最近我的很多学生在跟我吐槽学数学时遇到的疑难杂症:
·课后笔记追记不错,但学校2次考试,都只考了四五十分;
·上课听不懂,做题没思路;
·上课感觉听懂了,做题也感觉很会,但出错率奇高。
……

我跟他们做了一对一交流。像遇到第一个问题的学生,是个高中生。我给他一个建议,让他去把课程内容,自己重新推导一遍。一周后他考试成绩提升了30分。
不是我厉害,是找到问题的本质出在哪儿后,解决其实并不困难。找不到问题的本质,就有点像无头苍蝇一样乱转,假勤奋。感动了自己,也拿不到成果。
所以我希望给大家一个清晰的概念:数学学习核心的“点”在哪。
所有学不好数学的孩子,其实归根结底就是两大原因:第一,没有学“懂”;第二,没有养成好习惯。
学不好数学,本质原因之一:
没有学“懂”
什么是没有学懂”?
“懂”好像是个很模糊的说法,但我把“懂”分成了6个具体层级。
第一层级,知道认同。
有个特别具体的例子。前两天我跟外甥女交流。她已经四年级了。因为我看她作业里乘法分配律错了不少,就跟她讲乘法分配率的原理。
讲着讲着,我发现,她不光乘法分配率的原理不知道,她连乘法的原理都不知道。
比如2乘以3什么意思?她不知道。我花了一个小时间给她讲2乘以3,是3个2相加,或者是2个3相加。——可想而知,她在学校听的是什么。
这就是“知道认同”,孩子觉得老师讲得挺有道理——反正老师讲的都对,但是她其实是不理解的。

《请回答1988》剧照
第二层级,理解含义。
他知道这是什么,但不会用。这样的情况也挺多的。
第三层级,能够应用。
理解了,能够用。很多孩子停留在这个层级了。
第四层级,知其所以然。
他既知道是什么,也知道为什么,来龙去脉是怎样的。
第五层级,能迁移其所以然。
孩子能迁移到别的知识上去,这就要求他懂得知识之间的联系。
第六层级,能迁移背后的数学思想/哲学思想。
举个例子。很多孩子能在平面直角坐标系上,找到一个点的坐标。但你再给他个空间直角坐标系,完全懵了。
原因就是,他只“懂”了前三个层级,但到第四个层级,——为什么一个点的坐标是往左和往下各做一条垂线,他就不知道。
如果他知道这个原理,遇上空间直角坐标系,那他就同样知道可以往三个坐标轴做垂线,找到坐标。这就是能够迁移,背后是转化的思想。

为什么我强调孩子“懂”的层级?
他理解到什么程度,决定了能举一反三到什么程度。他是同类的题会做,还是说连同一思想的题都会做?举一反三的范围,不一样。
反过来,他如果连为什么这个知识点是这样的,都没搞清楚,你要他去迁移,根本不可能。因为他看到的就是不同的东西,而不是它们共同的本质。能看到本质,一定是理解到背后的“为什么”,或者共同的数学思想。
其实,大部分学生“懂”的层级都没有超过前三级,这就是为什么很多孩子数学得吃力。他没想明白一个数学做法背后的原理,只能说学到什么用什么,那学的东西一多,自然效率就不够,时间就不够,数学就成了一件很难的事情。
学不好数学,本质原因之二:
没好习惯
接下来我们讲习惯问题。
很多家长说,孩子总是计算扣分,是马虎吗,粗心吗?答案肯定不是。
因为你一次不小心,那是不小心。你次次不小心,总不能说自己总是不小心吧?本质还是习惯没有养成。
那首先,我们需要界定清楚,什么是学习上的好习惯?
我把大家普遍认为的好习惯列一下:课前预习、认真听课、做错题本,还有每天练一些计算题。但这些,我觉得都称不上是好习惯。
为什么我这么说?
举一个最简单的例子,认真听课是好习惯吗?在我看来,认真听课只是个形式,谈不上说是一个好习惯。
因为我刚才讲,“懂”分六个层级,认真听课,很可能就只停留在第一个层级“知道认同”。
看起来他恨不得把老师讲的每个字都抓到耳朵里,但问题的核心是他的脑子有没有开动呢?有没有思考清楚来龙去脉,会不会迁移?如果没有,确实谈不上好习惯。
再比如说做错题本。前两天有个家长给我发消息,他孩子六年级的,数学考了70多分,然后学校老师让他把错题抄一遍,并要求家长监督。
这在我看来,其实也很难奏效。如果没有理解做错的原因,抄错题只是形式,浪费时间而已,假性勤奋。
还有家长说,孩子计算不好,就要多练习,每天练个5道、10道。同理,这也是形式而已。对提升正确率有没有帮助?
说实话,如果你的孩子正好是什么习惯都好,只是熟练度不够,这个方法是有帮助的。
但很多孩子并不是熟练度的问题,而是习惯不好,比如计算乱涂乱改、跳步、不打草稿等等,这才是真问题。

如果不认识到这些问题去改这些习惯,甚至有的家长还限时掐表,要求做题速度,你想想这是在强化孩子的正确习惯,还是在强化他错误的原有习惯?稍微一想就知道,只是海量练习,算不上一个解决问题的好办法。
所以什么叫好习惯?
好习惯,不仅仅是你做了某件事,更重要的是你怎么完成这件事的。所以我们强调的好习惯,更多时候要充满细节。
以计算习惯为例。
比如,很多孩子不打草稿,为什么?因为在他眼里面,打草稿又浪费时间,又很费劲,所以他不爱打草稿。
那什么是计算习惯的细节?我们看下面这道题,只看分子:
你发现没有,-2(x-1)²,这一步要算两步。而后面那几个括号只需要算一步,在这种情况下,我们就可以这样规划,把需要算两步的打在草稿纸上。
这样做有什么好处呢?首先,他并没有多算,不会浪费时间,也解决了跳步的问题。同时以防他要把每一步骤都列上去,导致抄写繁杂,易出错。
所以孩子没有理解的是,打草稿其实是控制计算节奏。有点像弹钢琴,保证节拍。这就是一个计算的习惯,它是一个细节。
我给清北班的学生上第一节课,就讲怎么计算,有很多细节。包括:数字怎么书写;打草稿的时候怎么排版;草稿纸怎么用;哪些步能跳步,哪些步不能跳……都是要讲清楚的。因为这些东西影响他计算的正确率。
所以不是那么简单地说,“你多算几遍”,或者“你细心一点”,就能够帮他减少计算错误率,没有那么简单。
计算习惯,是肌肉记忆,有点像跳舞。你看到舞台上的舞者,姿势优美,身材轻盈,跳一场舞酣畅淋漓。那是每天专项训练,无数细节融合而成的肌肉习惯。这个咱们看不到的,看到的只是最后呈现出来的样子。
同样,在计算上,很多人只看到最后计算呈现出来的就是100%正确率或者90%正确率。但是这些正确率背后就是由一个一个的细节组成的。如果不去调整细节习惯,那很多时候再怎么练习,也很难拿到好结果。

《天才谢尔顿》剧照
计算这样,审题习惯也是。
很多学生觉得审题就是打个圈,甚至连圈都不打。他相信自己目光如电,一扫而过,整个题都印到了我心中。那才见鬼。怎么可能?
数学里边的审题是有很大讲究的。你读古文是不是有一种感觉,文需字字读,要是漏一个字,可能意思理解就不对了。因为我们知道,古文的含义是特别丰富的。
其实,数学语言更是世界上最简洁的语言,数学的题目更加是,“文需字字读”。他如果只是简单扫一遍题目,或者简单画个圈什么的,根本没有办法解读出背后隐藏的信息。
我给大家做个示范,如下图。数学题目是要做翻译的,每一句数学题目的文字语言,都需要翻译成数学语言。
再比如说总结习惯。很多家长说,我们家孩子初二,前面学得还好好的,为什么一学到全等三角形,全不明白了。
我说,不明白就对了。为什么说初二开始两极分化,就是卡在全等三角形这个章节?因为全等三角形是几何证明的真正开始。
所有的代数,你如果做翻译的话,会发现它只有一个翻译,基本上方向是唯一的。但几何一个条件,比如说中点,可以去想中位线,可以想三线合一,还可以想背长中线法,还还可以想三线斜边中点。每一个条件它都有很多种可能性,这都需要总结。
如果他没有做好总结,不知道各种可能性怎么去思考运用,那么就不太可能在考场的有限时间内,找到那个思路。
就跟走迷宫一样,一个口有多少条岔路,一条一条去试,没那个时间,对吧?碰运气的话,大概率也碰不到。
所以这时候,他一定要有总结的习惯。所以到初二没有学会总结的学生,不去追究这个辅助线为什么这么做的学生,几何很难学好。
当然,除了计算、审题、总结习惯以外,还有很多别的习惯,比如说研究的习惯、听课的习惯、课后笔记追记的习惯等等。每个习惯怎么做,都有很多细节。

好习惯本质是提升他的学习效率和得分效率的。而好习惯都在细节里。可以说,习惯,就是关于细节的。它要变成肌肉记忆,变成孩子一个做事的流程。
但也有句话说得好,懂了这么多道理,仍然过不好这一生。习惯也不容易养成。如果说用一句话总结,习惯养成的核心秘诀是什么?
习惯养成的本质,就是“高频重复”。
高音歌唱家杨洋曾说,同样上10节课,你每天上1节课的效果,远远强于你分10周每周上1节课的效果。习惯的核心就是高频。
怎么解决当前数学课堂存在的问题?
很多数学课存在什么问题呢?
第一,以老师讲解为主,学生听课为主,缺乏主动思考。
第二,弱化概念和推导,强化刷题,学生不会举一反三。
第三,就是对习惯养成,以强调为主,少有行动,没有具体的细节操作可以帮助孩子落地。只是空说,能落地的可能性不是很大。
基于这些问题,孩子在理解的层次上,最多在我们前面讲的“懂”前两三个层级晃荡。
那我认为,好的课堂是怎样的呢?简单分享下。
第一,课上以学生为中心,概念由学生定义,公式由学生推导,例题解答和总结也是学生先做,强互动。
所以,我上一堂课,可能就讲1/3时间。怎么知道孩子在这段时间有没有思考呢?有一个守门员,叫笔记追记。
什么叫笔记追记?就是我们要求,上课学生不能做笔记,课后再去做追记。也就是说,根据学过的内容,自己去推导一遍。
这个时候,学生不可能靠死记硬背,只能自己推导,那至少达到了知其所以然的要求,避免只是“自己觉得听懂了”,然后混过去。
第二,要达到能迁移,老师就必须要强调知识间的联系。
比如,这堂课的知识点是正负数相加,它的原理是什么?很多同学会背正数加正数就是绝对值相加,负数加负数就是取负号,绝对值相加等等。这样还是死记硬背,不会迁移运用知识的,学不活。
那我会带学生怎么做呢?画一个数轴,用有方向的线段来表示,那么正3加负2,我们是往右跳3格,往左跳2格,这样学生就能理解,它为什么是这么算。
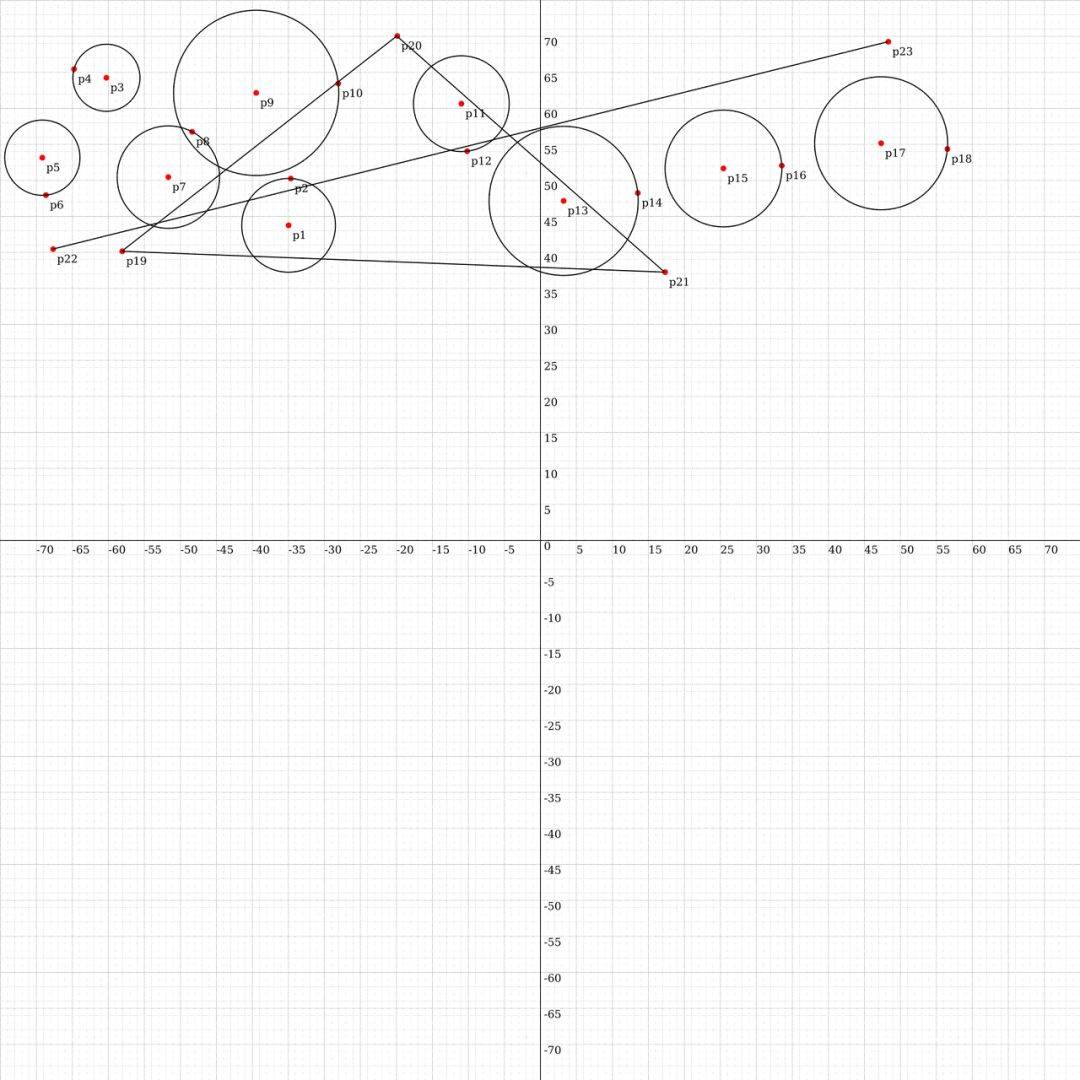
当我们这么考虑正负数加法的时候,其实已经是一个最简单的同方向或者反方向的线段加法,也就是我们高中所谓的“向量加法”了。
那我们继续考虑,如果这两个不在同一方向或者相反方向,还能相加吗?根据转化的思想原理,不是同一方向,能不能转化到同一方向呢?所以就把这两个斜着的线段转化成了水平和竖直的,它们就能相加了,这就是数学思想的迁移。
除了 每一堂课的知识点强调前后联系,我们还会 在知识模块上去强调前后联系。
以我们的代数课为例,先后涉及到知识点分别是,乘法公式、竖式除法、因式分解……一直到后面的一元二次方程和分式根式方程。有的家长会想说,现在我孩子才初一,校内没有学这些知识,孩子这么学完,会不会忘掉呢?不会的。
因为整式乘法公式是竖式除法的基础,竖式除法是因式分解的基础……也就是说, 孩子每学后面一个模块都会用到前面模块的知识。这就相当于,你最开始学的东西,它一直在练,而不是说学了这个知识之后,我就马上学另外一个知识,我就把它给忘掉了。
如果大家对人工智能有所了解,应该知道在训练过程中,训练素材的比例会影响效率。例如,当训练数据中旧材料占85%,新材料占15%时,往往能达到最高的效率。
其实对于学生来说也是一样,当新旧知识的比例达到80%比20%,甚至85%比15%的时候,他的学习效率是最高的。他会感觉,每一节课,都是旧知识稍微变了一下,长出来一个新知识,这就会比较适合学习曲线,学习效率会高一些。

最后,我还非常强调,数学思想和哲学思想。
说到这些东西,可能很多家长会觉得特别悬。到底什么叫数学思维呢?
首先, 训练数学思想的最简单的办法就是,一题多解、多解归一,还有多题一解、多题归一。什么意思呢?
我拿一个学生例子。这是个深圳学生,上初三,但他已经上完高中内容,而且也通过了当地的直升考试。
他发过来的是,他的课后追记。比如里面有“正难则反”的数学思想,怎么反?
总结了5种“反”的方法:反证法,逆推,先猜后证,还有待定系数法。
那具体每一种数学方法都是什么时候用?通过这个孩子总结的思维导图就能看出来。
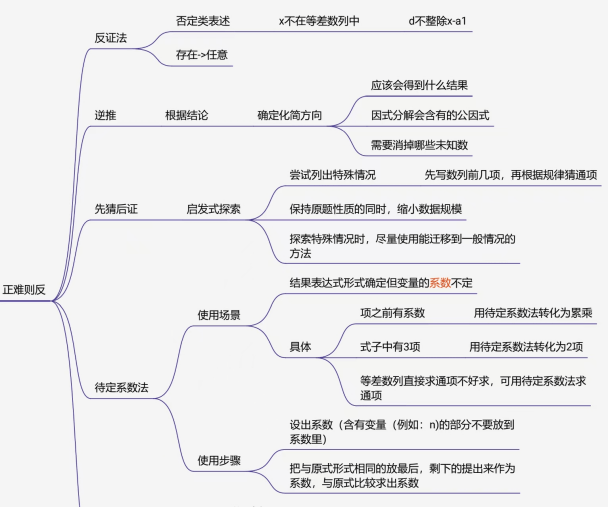
也就是说,我们对数学思想的理解也好,解读也好,它不是简单地,我告诉你一个什么思想,然后你做这道题就用这个思想,这太悬了。
而是说,每一个知识点背后都有数学思想,每一个数学方法背后也都有数学思想。怎么总结提炼呢?通过刚才讲的,一题多解、多解归一、多题归一。
其实,整个小学、初中、高中一共就十一二种数学思想,那么我们要做的,就是带着孩子不仅把握了这些数学思想,而且把握了实现这些数学思想的各种工具,各种方法,各种知识点。这个时候他的数学思想才是活的。

《天才基本法》剧照










